(Original article by Philip Ball, aeon.co)
Why can we count to 152? OK, most of us don’t need to stop there, but that’s my point. Counting to 152, and far beyond, comes to us so naturally that it’s hard not to regard our ability to navigate indefinitely up the number line as something innate, hard-wired into us.
Scientists have long claimed that our ability with numbers is indeed biologically evolved – that we can count because counting was a useful thing for our brains to be able to do. The hunter-gatherer who could tell which herd or flock of prey was the biggest, or which tree held the most fruit, had a survival advantage over the one who couldn’t. What’s more, other animals show a rudimentary capacity to distinguish differing small quantities of things: two bananas from three, say. Surely it stands to reason, then, that numeracy is adaptive.
But is it really? Being able to tell two things from three is useful, but being able to distinguish 152 from 153 must have been rather less urgent for our ancestors. More than about 100 sheep was too many for one shepherd to manage anyway in the ancient world, never mind millions or billions.
The cognitive scientist Rafael Núñez of the University of California at San Diego doesn’t buy the conventional wisdom that ‘number’ is a deep, evolved capacity. He thinks that it is a product of culture, like writing and architecture.
**
Numerical ability is more than a matter of being able to distinguish two objects from three, even if it depends on that ability. No non-human animal has yet been found able to distinguish 152 items from 153. Chimps can’t do that, no matter how hard you train them, yet many children can tell you even by the age of five that the two numbers differ in the same way as do the equally abstract numbers 2 and 3: namely, by 1.
What seems innate and shared between humans and other animals is not this sense that the differences between 2 and 3 and between 152 and 153 are equivalent (a notion central to the concept of number) but, rather, a distinction based on relative difference, which relates to the ratio of the two quantities. It seems we never lose that instinctive basis of comparison.
**
According to Núñez, is that the brain’s natural capacity relates not to number but to the cruder concept of quantity. ‘A chick discriminating a visual stimulus that has what (some) humans designate as “one dot” from another one with “three dots” is a biologically endowed behaviour that involves quantity but not number,’ he said. ‘It does not need symbols, language and culture.’
**
Although researchers often assume that numerical cognition is inherent to humans, Núñez points out that not all cultures show it. Plenty of pre-literate cultures that have no tradition of writing or institutional education, including indigenous societies in Australia, South America and Africa, lack specific words for numbers larger than about five or six. Bigger numbers are instead referred to by generic words equivalent to ‘several’ or ‘many’. Such cultures ‘have the capacity to discriminate quantity, but it is rough and not exact, unlike numbers’, said Núñez.
That lack of specificity doesn’t mean that quantity is no longer meaningfully distinguished beyond the limit of specific number words, however. If two children have ‘many’ oranges but the girl evidently has lots more than the boy, the girl might be said to have, in effect, ‘many many’ or ‘really many’. In the language of the Munduruku people of the Amazon, for example, adesu indicates ‘several’ whereas ade implies ‘really lots’. These cultures live with what to us looks like imprecision: it really doesn’t matter if, when the oranges are divided up, one person gets 152 and the other 153. And frankly, if we aren’t so number-fixated, it really doesn’t matter. So why bother having words to distinguish them?
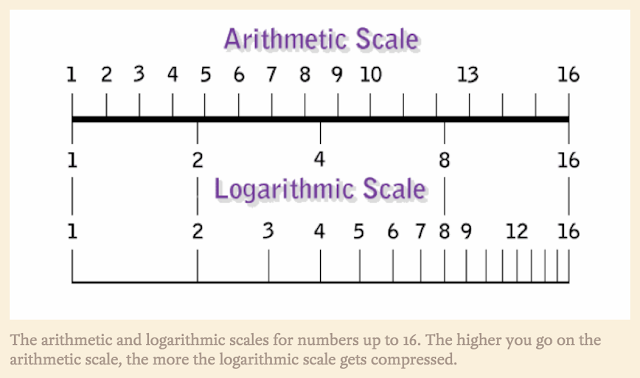
Some researchers have argued that the default way that humans quantify things is not arithmetically – one more, then another one – but logarithmically. The logarithmic scale is stretched out for small numbers and compressed for larger ones, so that the difference between two things and three can appear as significant as the difference between 200 and 300 of them.
**
In 2008, the cognitive neuroscientist Stanislas Dehaene of the Collège de France in Paris and his coworkers reported evidence that the Munduruku system of accounting for quantities corresponds to a logarithmic division of the number line. In computerised tests, they presented a tribal group of 33 Munduruku adults and children with a diagram analogous to the number line commonly used to teach primary-school children, albeit without any actual number markings along it. The line had just one circle at one end and 10 circles at the other. The subjects were asked to indicate where on the line groupings of up to 10 circles should be placed.
Whereas Western adults and children will generally indicate evenly spaced (arithmetically distributed) numbers, the Munduruku people tended to choose a gradually decreasing spacing as the numbers of circles got larger, roughly consistent with that found for abstract numbers on a logarithmic scale. Dehaene and colleagues think that for children to learn to space numbers arithmetically, they have to overcome their innately logarithmic intuitions about quantity.
Attributing more weight to the difference between small than between large numbers makes good sense in the real world, and fits with what Fias says about judging by difference ratios. A difference between families of two and three people is of comparable significance in a household as a difference between 200 and 300 people is in a tribe, while the distinction between tribes of 152 and 153 is negligible.
It’s easy to read this as a ‘primitive’ way of reasoning, but anthropology has long dispelled such patronising prejudice. After all, some cultures with few number words might make much more fine-grained linguistic distinctions than we do for, say, smells or family hierarchies. You develop words and concepts for what truly matters to your society. From a practical perspective, one could argue that it’s actually the somewhat homogeneous group of industrialised cultures that look odd, with their pedantic distinction between 1,000,002 and 1,000,003.
Whether the Munduruku really map quantities onto a quasi-logarithmic division of ‘number space’ is not clear, however. That’s a rather precise way of describing a broad tendency to make more of small-number distinctions than of large-number ones. Núñez is skeptical of Dehaene’s claim that all humans conceptualise an abstract number line at all. He says that the variability of where Munduruku people (especially the uneducated adults, who are the most relevant group for questions of innateness versus culture) placed small quantities on the number line was too great to support the conclusion about how they thought of number placement. Some test subjects didn’t even consistently rank the progressive order of the equivalents of 1, 2 and 3 on the lines they were given.
‘Some individuals tended to place the numbers at the extremes of the line segment, disregarding the distance between them,’ said Núñez. ‘This violates basic principles of how the mapping of the number line works at all, regardless of whether it is logarithmic or arithmetic.’
Building on the clues from anthropology, neuroscience can tell us additional details about the origin of quantity discrimination. Brain-imaging studies have revealed a region of the infant brain involved in this task – distinguishing two dots from three, say. This ability truly does seem to be innate, and researchers who argue for a biological basis of number have claimed that children recruit these neural resources when they start to learn their culture’s symbolic system of numbers. Even though no one can distinguish 152 from 153 randomly spaced dots visually (that is, without counting), the argument is that the basic cognitive apparatus for doing so is the same as that used to tell 2 from 3.
But that appealing story doesn’t accord with the latest evidence, according to Ansari. ‘Surprisingly, when you look deeply at the patterns of brain activation, we and others found quite a lot of evidence to suggest a large amount of dissimilarity between the way our brains process non-symbolic numbers, like arrays of dots, and symbolic numbers,’ he said. ‘They don’t seem to be correlated with one another. That challenges the notion that the brain mechanisms for processing culturally invented number symbols maps on to the non-symbolic number system. I think these systems are not as closely related as we thought.’
If anything, the evidence now seems to suggest that the cause-and-effect relationship works the other way: ‘When you learn symbols, you start to do these dot-discrimination tasks differently.’
This picture makes intuitive sense, Ansari argues, when you consider how hard kids have to work to grasp numbers as opposed to quantities. ‘One thing I’ve always struggled with is that on the one hand we have evidence that infants can discriminate quantity, but on the other hand it takes children between two to three years to learn the relationship between number words and quantities,’ he said. ‘If we thought there was a very strong innate basis on to which you just map the symbolic system, why should there be such a protracted developmental trajectory, and so much practice and explicit instruction necessary for that?’
But the apparent disconnect between the two types of symbolic thought raises a mystery of its own: how do we grasp number at all if we have only the cognitive machinery for the cruder notion of quantity? That conundrum is one reason why some researchers can’t accept Núñez’s claim that the concept of number is a cultural trait, even if it draws on innate dispositions. ‘The brain, a biological organ with a genetically defined wiring scheme, is predisposed to acquire a number system,’ said the neurobiologist Andreas Nieder of the University of Tübingen in Germany. ‘Culture can only shape our number faculty within the limits of the capacities of the brain. Without this predisposition, number symbols would lie [forever] beyond our grasp.’
‘This is for me the biggest challenge in the field: where do the meanings for number symbols come from?’ Ansari asks. ‘I really think that a fuzzy system for large quantities is not going to be the best hunting ground for a solution.’
Perhaps what we draw on, he thinks, is not a simple symbol-to-quantity mapping, but a sense of the relationships between numbers – in other words, a notion of arithmetical rules rather than just a sense of cardinal (number-line) ordering. ‘Even when children understand the cardinality principle – a mapping of number symbols to quantities – they don’t necessarily understand that if you add one more, you get to the next highest number,’ Ansari said. ‘Getting the idea of number off the ground turns out to be extremely complex, and we’re still scratching the surface in our understanding of how this works.’
The debate over the origin of our number sense might itself seem rather abstract, but it has tangible practical consequences. Most notably, beliefs about the relative roles of biology and culture can influence attitudes toward mathematical education.
The nativist view that number sense is biological seemed to be supported by a 2008 study by researchers at the Johns Hopkins University in Baltimore, which showed 14-year-old test subjects’ ability to discriminate at a glance between exact numerical quantities (such as the number of dots in an image) correlated with their mathematics test scores going back to kindergarten. In other words, if you’re inherently good at assessing numbers visually, you’ll be good at maths. The findings were used to develop educational tools such as Panamath to assess and improve mathematical ability.
via Aeon